CompSci Collaborators, Topics
Dong Ahn ,
Dylan Chapp
,
Dylan Chapp ,
Mario Guevara
,
Mario Guevara ,
Joy Kitson
,
Joy Kitson ,
Ricardo Llamas
,
Ricardo Llamas ,
Kento Sato
,
Kento Sato ,
Michela Taufer
,
Michela Taufer ,
Rodrigo Vargas
,
Rodrigo Vargas
With the
Global Computing Lab, my research was primarily on the following two projects: (1)
Applying machine learning methods to soil moisture data, to fill gaps
and downscale resolution; (2) Modeling and analyzing nondeterminism in
executions of parallel programs, especially involving MPI.
Math Collaborators, Topics
Zhanar Berikkyzy ,
Anton Bernshteyn
,
Anton Bernshteyn ,
Beth Bjorkman
,
Beth Bjorkman ,
Axel Brandt
,
Axel Brandt ,
Garner Cochran
,
Garner Cochran ,
Joshua Cooper
,
Joshua Cooper ,
Wei Gao
,
Wei Gao ,
Sylvia Hobart
,
Sylvia Hobart ,
Sogol Jahanbekam
,
Sogol Jahanbekam ,
Bill Kay
,
Bill Kay ,
Lauren Keough
,
Lauren Keough ,
Omid Khormali
,
Omid Khormali ,
Rachel Kirsch
,
Rachel Kirsch ,
Victor Larsen
,
Victor Larsen ,
Ryan Martin
,
Ryan Martin ,
Brent McKain
,
Brent McKain ,
Kevin Moss
,
Kevin Moss ,
Mitch Phillipson
,
Mitch Phillipson ,
Jonathan Rollin
,
Jonathan Rollin ,
Songling Shan
,
Songling Shan ,
Heather Smith
,
Heather Smith ,
Claude Tardif
,
Claude Tardif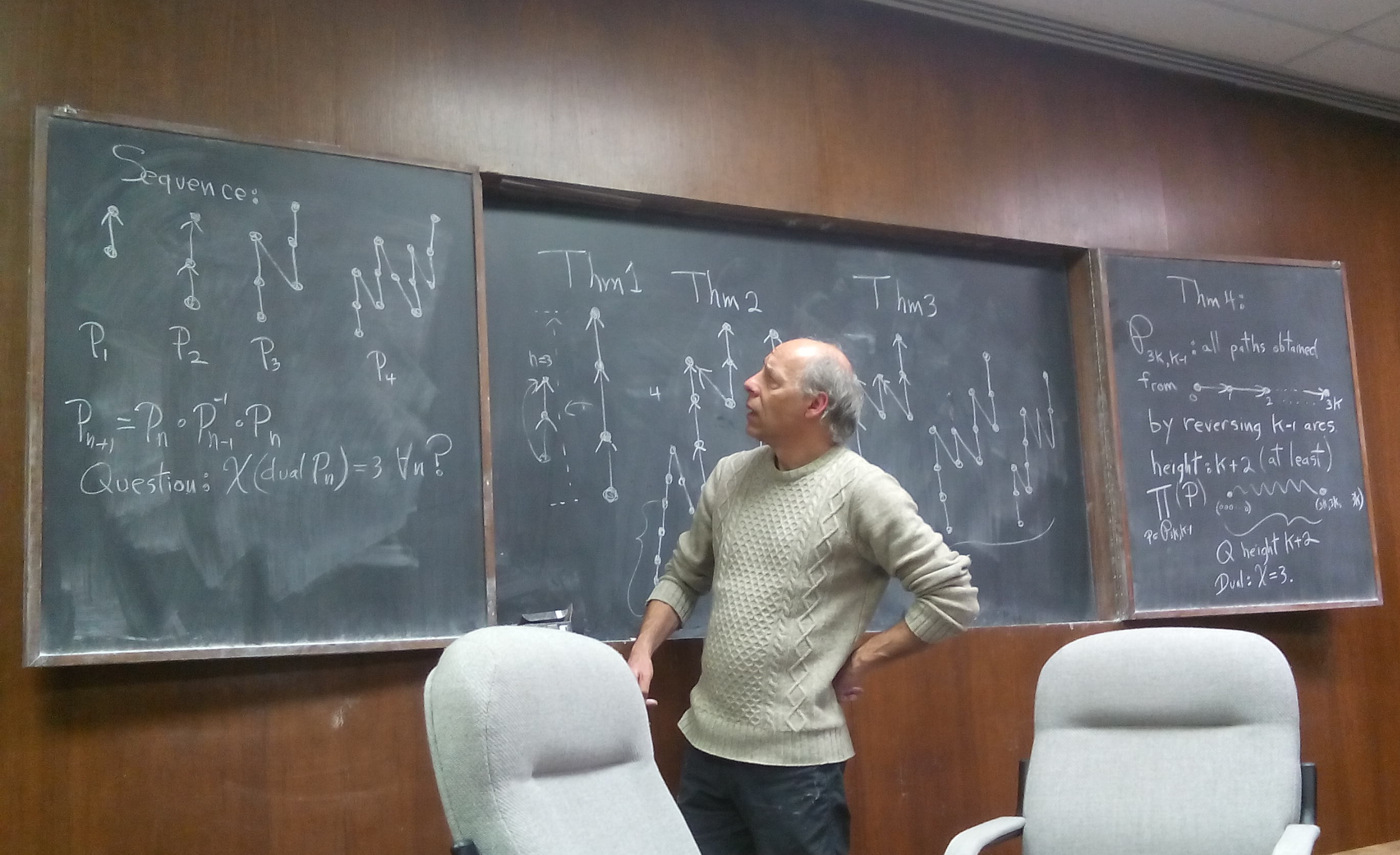 ,
David Wehlau
,
David Wehlau ,
Andrew Uzzell
,
Andrew Uzzell ,
Jennifer Wise
,
Jennifer Wise ,
Imed Zaguia
,
Imed Zaguia
My main mathematical interests lay in combinatorics on words, graph
theory, discrete geometry, combinatorial limit theory, and
applications of discrete mathematics to linguistics.
Scholarship
-
Published Papers
-
(with Berikkyzy, Brandt, Jahanbekam, Larsen) "Antimagic Labelings
of Weighted Graphs."
Discrete Mathematics & Theoretical Computer Science
23(3), December 2021. [DOI (DMTCS);
arXiv]
-
(with Bernshteyn, Khormali, Martin, Rollin, Shan, Uzzell) "Regular
colorings of regular graphs."
Discussiones Mathematicae Graph Theory 4(3), April
2020. [Sciendo;
DOI (DMGT);
arXiv]
-
(with Llamas, Guevara, Taufer, Vargas) "Spatial Gap-Filling of ESA
CCI Satellite-Derived Soil Moisture Based on Geostatistical
Techniques and Multiple Regression." Remote Sensing
12(4), February 2020. [DOI (MDPI);
DOI (Preprints)]
-
"A bound on a convexity measure for point sets."
International Journal of Computational Geometry and
Applications
29(4)301-306, December 2019. [DOI (IJCGA);arXiv]
-
(with Chapp, Sato, Ahn, Taufer) "A three-phase workflow for
general and expressive representations of nondeterminism in HPC
applications."
International Journal of High Performance Computing
Applications
33(6)1175-1184, November 2019. [DOI (Sage)]
-
(with Guevara, Llamas, Kitson, Vargas, Taufer) "SOMOSPIE: A
modular SOil MOisture SPatial Inference Engine based on data
driven decisions." 15th eScience, September 2019. [DOI (IEEE);
arXiv]
-
"Graph cover-saturation." Graphs and Combinatorics
35(5)1225--1237, September 2019. [DOI;
arXiv]
-
(with Bjorkman, Cochran, Gao, Keough, Kirsch, Philipson, Smith,
Wise) "\(k\)-foldability of words."
Discrete Applied Mathematics 259:19--30, April 2019.
[DOI (ScienceDirect);
arXiv]
-
(with Tardif, Wehlau, Zaguia) "Iterated arc graphs."
Commentationes Mathematicae Universitatis Carolinae
59(3)277--283, 2018. [DOI (DML-CZ);
CMUC;
arXiv]
-
(with Cooper) "Density dichotomy in random words."
Contributions to Discrete Mathematics 13(1), January
2018. [DOI (UCalgary);
arXiv]
-
(with Tardif, Wehlau) "Logical compactness and constraint
satisfaction problems."
Logical Methods in Computer Science 13(1)#1:1--11,
January 2017. [LMCS;
arXiv]
-
(with Cooper) "Asymptotic Density of Zimin Words."
Discrete Mathematics & Theoretical Computer Science
18(3)#3, March 2016. [DMTCS;
arXiv]
-
"Toward the Combinatorial Limit Theory of Free Words." University
of South Carolina Dissertation, August 2015. [arXiv]
-
(with Cooper) "Bounds on Zimin Word Avoidance."
Congressus Numerantium 222:87--95, 2014. [arXiv]
-
Peer-Reviewed Abstracts and Posters
-
In Preparation
-
(with Berikkyzy, Bjorkman, Hobart, Jahanbekam, Kay, Keough,
McKain, Moss, Shan, Smith) "Triangle-distinct graphs."
-
Other
-
"Arabic Influence on the Spanish Language." Research paper for
B.S. in Linguistics, Seattle Pacific University, May 2010. [pdf]
-
"Collatz Generalized." Research Paper for B.S. in Mathematics,
Seattle Pacific University, May 2010. [pdf]
Invited Talks (
show abstracts)
-
"Cyberinstractures for Scientific Discovery with Emphasis on Wildfire
Simulations" (40 min). Fire Research Division seminar, National
Institute of Standards and Technology (NIST), Gaithersburg. 20 March
2019.
-
"A Workflow for Soil Moisture Analytics" (20 min). Innovative
Computing Laboratory seminar, University of Tennessee at Knoxville. 15
March 2019.
-
"Integer Sequences" (50 min). Mathematics and Statistics Colloquium,
Colby College. 11 October 2018. [seminar schedule]
-
"Graph domination-saturation" (50 min). Combinatorics, Algebra, and
Topology Seminar, United States Naval Academy. 23 April 2018. [seminar schedule]
-
"Combinatorial Nullstellensatz in Graph Theory" (20 min), Special
Session on Advanced Techniques in Graph Theory. AMS Sectional Meeting,
University of Buffalo. 17 September 2017. [program listing]
-
"Bridging Logic and Constraint Satisfaction with Relational Structures
and Filters" (60 min). Logic and Combinatorics Seminars (combined),
McGill University. 4 November 2016.
-
"Antimagic Graphs and Combinatorial Nullstellensatz" (60 min).
Graduate Seminar, University of Colorado Denver. 29 September 2014.
-
"Collatz Generalized: An Expansion of the \(3x + 1\) Problem" (25
min). 11th Carolina Math Seminar, Benedict College. 2 February
2012. [video]
Invited Talks (
hide abstracts)
-
"Cyberinstractures for Scientific Discovery with Emphasis on Wildfire
Simulations" (40 min). Fire Research Division seminar, National
Institute of Standards and Technology (NIST), Gaithersburg. 20 March
2019.
This talk presents cyberinfrastructure (i.e., research environments,
software, hardware, and services) that can augment fire simulation
efforts. We survey a holistic approach to scientific modeling,
including data integration and production, utilization of modern
high performance computing (HPC) and cloud computing, and
implementation of portable application program interface (API)
technology. In particular, we will discuss our experience and
available resources at UTK for these components and their potential
for expanding and enhancing the wildfire simulation capabilities of
NIST.
This is joint work with David Icove, Michela
Taufer, Michael Jantz, and Stephen Marz.
-
"A Workflow for Soil Moisture Analytics" (20 min). Innovative
Computing Laboratory seminar, University of Tennessee at Knoxville. 15
March 2019.
In this talk we present a general cyberinfrastructure workflow for
scientific simulation that can support precision farming. Our
workflow incorporates data integration and production at the edge,
utilization of cloud and high performance computing for the
analytics, and implementation of portable application program
interface (API) technology for the users. In particular, we will
zoom in on a HYbrid Piecewise POlynomial (HYPPO) modeling technique
and the role it plays in one stage of the workflow surrounding a
problem in soil moisture analytics associated to fine-grained
predictions.
-
"Integer Sequences" (50 min). Mathematics and Statistics Colloquium,
Colby College. 11 October 2018. [seminar schedule]
The powers of 2: \(\{1, 2, 4, 8, 16, 32, 64, \ldots\}\). The maximum
number of regions obtained when slicing a circle with \(n\) lines:
\(\{1, 2, 4, 7, 11, 16, 22, 29,\ldots \}\). Integer sequences are
found throughout mathematics, but especially in number theory and
combinatorics. They might count a class of mathematical objects or
just have fascinating numerical properties. What is the rule for
constructing the following sequence: \(\{1, 2, 2, 1, 1, 2, 1, 2, 2,
1, 2, 2, 1, 1, 2, 1, 1, 2, 2, \ldots \}\)?
The number of neutrons in the most abundant isotope of each element
on the periodic table: \(\{0, 2, 4, 5, 6, 6, 7, 8, 10, 10, 12,
\ldots\}\). The year in which the population of earth reached \(n\)
billion: \(\{1804, 1927, 1959, 1974, 1987, 1999, 2011(, \ldots? )
\}\). Integer sequences are everywhere. Can you figure out what this
sequence represents: \(\{3, 3, 5, 4, 4, 3, 5, 5, 4, 3, 6,
\ldots\}\)?
In this talk, we share the joys of studying integer sequences and
tools available for investigation. With sequences, you can practice
programming and make connections between disciplines; they are the
source of both silly puzzles and deep, unsolved mathematical
questions.
-
"Graph domination-saturation" (50 min). Combinatorics, Algebra, and
Topology Seminar, United States Naval Academy. 23 April 2018. [seminar schedule]
Graph \(G\) is \(F\)-saturated if \(G\) contains no copy of graph
\(F\) but any edge added to \(G\) produces at least one copy of
\(F\). One common variant of saturation is to remove the former
restriction: \(G\) is \(F\)-semi-saturated if any edge added to
\(G\) produces at least one new copy of \(F\). In this paper we take
this idea one step further. Rather than just allowing edges of \(G\)
to be in a copy of \(F\), we require it: \(G\) is \(F\)-dominated if
every edge of \(G\) is in a copy of \(F\). It turns out that there
is smooth interaction between domination and semi-saturation, which
opens for investigation a natural analogue to saturation numbers.
Therefore we present preliminary domination-saturation theory and
structural bounds for the domination-saturation numbers of graphs.
We also establish asymptotic domination-saturation densities for
cliques and paths, and upper and lower bounds (with small gaps) for
cycles and stars. [arXiv:1801.04250]
-
"Combinatorial Nullstellensatz in Graph Theory" (20 min), Special
Session on Advanced Techniques in Graph Theory. AMS Sectional Meeting,
University of Buffalo. 17 September 2017. [program listing]
Combinatorial Nullstellensatz is an algebraic technique developed by
Alon and Tarsi in 1992. Alon named this method in 2001 when he
demonstrated its applicability to a wide range of problems in
additive number theory and graph theory. This is an early instance
of what is now called the Polynomial Method, a general approach for
applying algebraic geometry to solve problems in discrete
mathematics. Roughly speaking, by strategically associating a
discrete structure or configuration with a polynomial, one can
utilize algebraic properties of the Nullstellen (zero locus). This
talk will focus on graph theoretic applications of Combinatorial
Nullstellensatz, especially to guarantee the existence of particular
subgraphs or labelings.
-
"Bridging Logic and Constraint Satisfaction with Relational Structures
and Filters" (60 min). Logic and Combinatorics Seminars (combined),
McGill University. 4 November 2016.
Relational structure \(\mathbb{A}\) is compact provided for any
structure \(\mathbb{B}\) of the same signature, if every finite
substructure of \(\mathbb{B}\) has a homomorphism to \(\mathbb{A}\)
then so does \(\mathbb{B}\). The Constraint Satisfaction Problem
(CSP) for \(\mathbb{A}\) is the computational problem of determining
whether finite structures have homomorphisms into \(\mathbb{A}\). We
explore a connection between the hierarchy of logical axioms and the
complexity hierarchy of CSPs: It appears that the complexity of the
CSP for \(\mathbb{A}\) corresponds to the strength of statement
"\(\mathbb{A}\) is compact" as an axiom. At the top, the statement
"\(K_3\) is compacts" is logically equivalent to the compactness
theorem. Thus the compactness of \(K_3\) implies the compactness of
all other finite relational structures. Moreover, the CSP for
\(K_3\) is NP-complete. At the bottom are the width-one structures;
these are provably complete with only ZF and their corresponding
CPSs are polynomial-time solvable.
This is joint work with
Claude Tardif and David Wehlau, arXiv:1609.05221 [math.LO].
-
"Antimagic Graphs and Combinatorial Nullstellensatz" (60 min).
Graduate Seminar, University of Colorado Denver. 29 September 2014.
A graph with m edges is antimagic provided there exists a labeling
of the edges with distinct integers from \(\{1,2,\ldots,m\}\) such
that, when each vertex is assigned the sum of the labels of its
incident edges, no two vertex sums are equal. In 1990, Hartsfield
and Ringel conjectured that every simple connected graph aside from
\(K_2\) is antimagic. In the last few years, a technique by Alon
called Combinatorial Nullstellensatz, has been used in proving
several results in the direction of this conjecture. Led by
Jahanbekam, a team from the Rocky Mountain-Great Plains Graduate
Research Workshop in Combinatorics has made great strides in this
problem toward the conjecture. The heart of this talk is a
demonstration of our particular use of Combinatorial
Nullstellensatz.
-
"Collatz Generalized: An Expansion of the \(3x + 1\) Problem" (25
min). 11th Carolina Math Seminar, Benedict College. 2 February
2012. [video]
The focus of this 2010 undergraduate research project is a
generalization of the Collatz conjecture, an unsolved number theory
problem involving the "\(3x+1\) function" on the positive integers:
if \(x\) is odd then \(C(x) = 3x + 1\); if \(x\) is even then \(C(x)
= \frac{x}{2}\). The Collatz conjecture is that, given any positive
integer \(x\), the infinite sequence \(\{x,C(x),C(C(x)),\ldots\}\)
-- the trajectory of \(x\) -- contains the number \(1\). Although
the conjecture has been proven for \(x\) up to at least \(10^{17}\),
it remains unproven for all positive integers. This project
investigates the problem within a broader context of the following
"\(Ax+B\) function": if \(x\) is odd then \(C(x) = Ax + B\); if
\(x\) is even then \(C(x) = \frac{x}{2}\). Under this wider scope,
the project explores the relationships between \(A\), \(B\) and
\(x\) and whether a trajectory contains \(1\), loops without
reaching \(1\), or is unbounded with no positive integer occurring
twice. Understanding these relationships may help to shed light on
why the trajectory of every positive integer under the \(3x+1\)
function contains \(1\), if such is in fact the case.
Citations
-
A. Carayol,
S. Göller, "On Long Words Avoiding Zimin Patterns."
Theory of Computing Systems, March 2019, special issue on
Theoretical Aspects of Computer Science (STACS 2017)
19:1–13 [DOI (TCS);
DOI (STACS);
arXiv];
-
D. Conlon,
J. Fox,
B. Sudakov. "Tower-type bounds for unavoidable patterns in words."
Transactions of the American Mathematical Society,
372:6213–6229, May 2019 [DOI;
arXiv]
-
J. Connor. "A Self-Referential Property of Zimin Words." [arXiv]
-
I. De Feis, "Optimal Interpolation for Infrared Products from Hyperspectral
Satellite Imagers and Sounders." Sensors 20(8), April
2020. [DOI]
-
E. Drellich
and
H. C. Smith, "Folding Words Around Trees: Models Inspired by RNA."
A Project-Based Guide to Undergraduate Research in Mathematics,
chapter 1, April 2020. [DOI]
-
A.Lozano,
M. Mora,
C. Seara. "Antimagic Labelings of Caterpillars."
Applied Mathematics and Computation, 347:734–740,
April 2019 [DOI]
-
N. Mhaskar,
M. Soltys. "Forced Repetitions over Alphabet Lists." [pdf]
-
W. Rytter,
A. Shur. "Searching for Zimin patterns."
Theoretical Computer Science 571:50–57, March
2015. [ACM DL]
-
S. Thomas. "Talk and Tradition: Connections between Language and
Culture in Igboland." [Academia]
Research Workshops and Summer Schools (Fully-funded Participant)
-
Argonne Training Program on Extreme-Scale Computing (ATPESC)
August 2018, Q Center, St. Charles, Illinois
-
São Paulo School of Advanced Science on Algorithms,
Combinatorics and Optimization (SPSAS-ACO)
July 2016, Instituto de Matemática e
Estatística, Universidade de São Paulo
-
LMS-CMI Research School, Regularity and Analytic Methods in
Combinatorics (RAMC)
July 2015, University of Warwick, Coventry
-
Rocky Mountain-Great Plains Graduate Research Workshop in
Combinatorics (GRWC 2015)
June 2015, Iowa State University, Ames
-
Rocky Mountain-Great Plains Graduate Research Workshop in
Combinatorics (GRWC 2014)
August 2014, University of Colorado Denver &
University of Denver
-
Graph Limits, Groups and Stochastic Processes
summer school
and
workshop
June 2014, MTA Rényi Institute of Mathematics,
Budapest
-
NSF Research Experience for Undergraduates,
UA VIGRE, Arizona Summer Program in Computational Photonics
July 2009, University of Arizona, Tucson
, Dylan Chapp
, Mario Guevara
, Joy Kitson
, Ricardo Llamas
, Kento Sato
, Michela Taufer
, Rodrigo Vargas

, Anton Bernshteyn
, Beth Bjorkman
, Axel Brandt
, Garner Cochran
, Joshua Cooper
, Wei Gao
, Sylvia Hobart
, Sogol Jahanbekam
, Bill Kay
, Lauren Keough
, Omid Khormali
, Rachel Kirsch
, Victor Larsen
, Ryan Martin
, Brent McKain
, Kevin Moss
, Mitch Phillipson
, Jonathan Rollin
, Songling Shan
, Heather Smith
, Claude Tardif
, David Wehlau
, Andrew Uzzell
, Jennifer Wise
, Imed Zaguia
